

题目链接: 高校排名
又是一道练习建模能力的题目, 算法同样很简单:SPFA最长路, 难在建模(也不算太难).
吐槽一下出题人的语文能力, 看了好几遍才懂题目意思
开始的想法是这样子的:
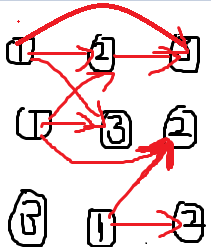
读入一行各大学专业排名, 如果 T[i] < T[j] 就连一条 i到j 的边,然后跑n遍 SPFA最长路(也可以设一个 超级源点), 最后求出 dis[n]的最大值。
但这样是不对的(╮(╯▽╰)╭), 因为只考虑了某专业的一行大学排名, 并没有兼顾其他行的排名, 比如上图中第一行 2->3 但在第二行 3在2的前面,虽然矛盾了,但我们仍然连接了 2到3 的一条边, 所以我们求出的结果总比正确结果大。
我们考虑这样建图:
申请一个 bFlag 数组。
读入一行各大学专业排名, 只要 i < j,就 bFlag[i][j] = true, 最后是这样子的:
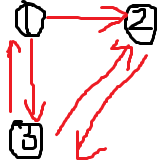
接下来我们按照条件连边,两个顶点 i, j, 只有 bFlag[i][j]=true 且 bFlag[j][i]=false 的情况下, 我们添加 i到j 的一条边. 这就满足了题目所要求的条件
考虑到答案 顶点数=边数+1 以及 只跑一遍SPFA最长路, 我们设立一个 超级源点,如下:
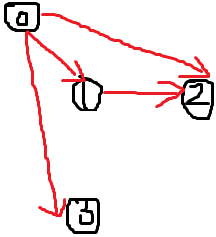
最后跑一遍 SPFA最长路 ,求出 dis[1…n] 中最大值即为答案。
/*
* Copyright © Eliot
* Date: 2016-10-26
* Author: Eliot
* QQ: 1161142536
* Description: 建模思想 SPFA最长路
*/
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
#define MAX 101
int Temp[MAX] = { 0 };
bool Is[MAX][MAX] = { false };
struct STRUCT{
int nPre;
int nTo;
}EDGE[1000 * MAX];
int head[MAX] = { 0 };
int nCount = 0;
void Add(int a, int b) {
EDGE[++ nCount].nTo = b;
EDGE[nCount].nPre = head[a];
head[a] = nCount;
}
queue<int> Q;
int dis[MAX] = { 0 };
bool IsStack[MAX] = { false };
void SPFA() {
Q.push(0);
IsStack[0] = true;
while (!Q.empty()) {
int nPoint = Q.front();
Q.pop();
IsStack[nPoint] = false;
for (int i = head[nPoint]; i != 0; i = EDGE[i].nPre) {
int nNextPoint = EDGE[i].nTo;
if (dis[nPoint] + 1 > dis[nNextPoint]) {
dis[nNextPoint] = dis[nPoint] + 1;
if (!IsStack[nNextPoint]) {
IsStack[nNextPoint] = true;
Q.push(nNextPoint);
}
}
}
}
}
int N = 0, M = 0;
int main() {
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; i ++) {
for (int j = 1; j <= N; j ++) scanf("%d", &Temp[j]);
for (int j = 1; j <= N; j ++) {
for (int k = j + 1; k <= N; k ++) {
Is[Temp[j]][Temp[k]] = true;
}
}
}
for (int i = 1; i <= N; i ++) {
for (int j = 1; j <= N; j ++) {
if (Is[i][j] && !Is[j][i]) {
Add(i, j);
}
}
}
for (int i = 1; i <= N; i ++) Add(0, i);
int ans = 0;
SPFA();
for (int i = 1; i <= N; i ++) ans = max(ans, dis[i]);
cout << ans << endl;
return 0;
}