23 Oct 2016 本文阅读量次

【Vijos 1626】爱在心中

一些无聊的概念之类的废话不再累赘，满满的全是干货！

Tarjan的作用就是求有向图中的强连通分量的个数，但是在很多题目中不只是数数强连通分量的个数就完事了， Tarjan经常是帮做一些别的事，比如2-sat、桥、割点等等.

裸 Tarjan 题(Vijos)：

信息传递(最后一个点Runtime，这题用Tarjan有点大材小用)
Victoria的舞会2
爱在心中(第一问，第二问要缩点)
裸 Tarjan 题不再废话了

结合爱在心中食用风味更加
题目链接：爱在心中

总体思路

题目中的图
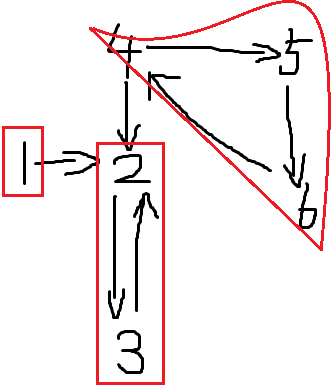
alt text

思路很清晰的一道题目，很明显的 Tarjan + 缩点。
如果Tarjan还不会的同学请移至隔壁CSDN博客学习。
主要说一下缩点，缩点在Tarjan中新增设一个数组为 Belong，来标识该强连通分量属于第几个强连通, 比如上图中2, 3属于一个强连通， 4, 5, 6属于一个强连通，则可以得：

Belong	Value
Belong[1]	1
Belong[2]	2
Belong[3]	2
Belong[4]	3
Belong[5]	3
Belong[6]	3

之后重新构图，求出缩点后每个强连通的出度，用数组P记录，如下：

P	Value
P[1]	1
P[2]	0
P[3]	1

之后遍历每个强连通分量，没有出度的那个强连通分量即为所求对象若有多个这样的强连通分量，则说明此图不连通，输出 -1 即可。

最后输出该强连通分量中的所有顶点。

Tarjan(带缩点) 代码注释：

int ans_Love = 0, ans_Love_T[MAX] = { 0 };

int Belong[MAX] = { 0 };
int P[MAX] = { 0 };

int DFN[MAX] = { 0 };
int LOW[MAX] = { 0 };
bool IsStack[MAX] = { 0 };
stack<int> Stack;
int nIndex = 0;

/***********************************
Name: Tarjan
Description: 求强连通分量(缩点) 
***********************************/
//事先初始化 for (int i = 1; i <= N; i++) Belong[i] = i;
void Tarjan(int nPoint) {
	DFN[nPoint] = LOW[nPoint] = ++ nIndex;    //更新DFN LOW 时间截
	IsStack[nPoint] = true;    //标记入栈
	Stack.push(nPoint);    //入栈
	
	for (int i = head[nPoint]; i != 0; i = EDGE[i].nPre) {    //邻接表遍历与nPoint相连点
		int nNextPoint = EDGE[i].nTo;    //目标点
		
		if (DFN[nNextPoint] == 0) {    //目标点没有被访问过
			Tarjan(nNextPoint);    //遍历点
			LOW[nPoint] = min(LOW[nNextPoint], LOW[nPoint]);    //更新LOW
		}
		else if (IsStack[nNextPoint]) {    //访问过目标点且目标点在栈中
			LOW[nPoint] = min(DFN[nNextPoint], LOW[nPoint]);    //更新LOW
		} 
	}
	
	int nTemp_count = 0, Temp = 0;
	if (DFN[nPoint] == LOW[nPoint]) {    //符合条件， 开始弹栈
		ans_Love ++;    //强连通个数
		do {
			Temp = Stack.top();    //取出栈顶元素
			Stack.pop();    //弹栈
			nTemp_count ++;

			Belong[Temp] = ans_Love;    //缩点
		} while (Temp != nPoint);
		ans_Love_T[++ nC] = nTemp_count;    //记录强连通内顶点数量
	}
}

缩点部分

/***********************************
Name: ReBuild 
Description: 重新构图 
***********************************/
void ReBuild() {
	for (int i = 1; i <= N; i++) {
		for (int j = head[i]; j != 0; j = EDGE[j].nPre) {
			int nNextPoint = EDGE[j].nTo;
			if (Belong[nNextPoint] != Belong[i]) P[Belong[i]] ++;    //处理两个强连通连接处(计算强连通分量的出度)
		}
	}
}

Main

// Tarjan 跑遍图
for (int i = 1; i <= N; i++) {
	if (DFN[i] == 0) Tarjan(i);
	memset(IsStack, false, sizeof(IsStack));
	nIndex = 0;
}
// 找出 “爱心天使”(去除顶点数为1的强连通分量)
for (int i = 1; i <= N; i ++) {
	if (ans_Love_T[i] > 1) ANS ++;
}
cout << ANS << endl;
// 重新构图
ReBuild();
//没有出度的那个强连通分量即为所求对象
//若有多个这样的强连通分量，则说明此图不连通
for (int i = 1; i <= ans_Love; i ++) {
	if (P[i] == 0 && ans_Love_T[i] > 1) {
		ans ++;
		nLast = i;
	}
}
if (ans > 1 || ans == 0) {
	printf("-1\n");
	return 0;
}

for (int i = 1; i <= N; i ++) {
	if (Belong[i] == nLast) printf("%d ", i);
}

完整代码

/*
* Copyright © Eliot
* Date: 2016-10-24
* Author: Eliot
* Description: Tarjan + 缩点(Vijos: P1626爱在心中)
* QQ: 1161142536
*/

#include <iostream>
#include <cstdio>
#include <stack>
#include <cstring>
using namespace std;

#define MAX 1001

int ans_Love = 0, ans_Love_T[MAX] = { 0 };
int nC = 0;

int N = 0, M = 0;
int a = 0, b = 0;

int Belong[MAX] = { 0 };
int P[MAX] = { 0 };

struct STRUCT {
	int nPre;
	int nTo;
}EDGE[10 * MAX];
int head[MAX] = { 0 };
int nCount = 0;

void Add(int a, int b) {
	EDGE[++nCount].nTo = b;
	EDGE[nCount].nPre = head[a];
	head[a] = nCount;
}

int DFN[MAX] = { 0 };
int LOW[MAX] = { 0 };
stack<int> Stack;
bool IsStack[MAX] = { 0 };
int nIndex = 0;

/***********************************
Name: Tarjan
Description: 求强连通分量(缩点) 
***********************************/
void Tarjan(int nPoint) {
	DFN[nPoint] = LOW[nPoint] = ++nIndex;
	IsStack[nPoint] = true;
	Stack.push(nPoint);

	for (int i = head[nPoint]; i != 0; i = EDGE[i].nPre) {
		int nNextPoint = EDGE[i].nTo;

		if (DFN[nNextPoint] == 0) {
			Tarjan(nNextPoint);
			LOW[nPoint] = min(LOW[nNextPoint], LOW[nPoint]);
		}
		else if (IsStack[nNextPoint]) {
			LOW[nPoint] = min(DFN[nNextPoint], LOW[nPoint]);
		}
	}

	int nTemp_count = 0, Temp = 0;
	if (DFN[nPoint] == LOW[nPoint]) {
		ans_Love ++;
		do {
			Temp = Stack.top();
			Stack.pop();
			nTemp_count ++;

			Belong[Temp] = ans_Love;
		} while (Temp != nPoint);
		ans_Love_T[++ nC] = nTemp_count;
	}
}

/***********************************
Name: ReBuild 
Description: 重新构图 
***********************************/
void ReBuild() {
	for (int i = 1; i <= N; i++) {
		for (int j = head[i]; j != 0; j = EDGE[j].nPre) {
			int nNextPoint = EDGE[j].nTo;
			if (Belong[nNextPoint] != Belong[i]) P[Belong[i]] ++;
		}
	}
}

int ANS = 0, ans = 0;
int nLast = 0;
int main() {
	scanf("%d %d", &N, &M);
	for (int i = 1; i <= M; i++) {
		scanf("%d %d", &a, &b);
		Add(a, b);
	}
	
	for (int i = 1; i <= N; i++) Belong[i] = i;
	
	for (int i = 1; i <= N; i++) {
		if (DFN[i] == 0) Tarjan(i);
		memset(IsStack, false, sizeof(IsStack));
		nIndex = 0;
	}
	for (int i = 1; i <= N; i ++) {
		if (ans_Love_T[i] > 1) ANS ++;
	}
	cout << ANS << endl;
	ReBuild();
	
	for (int i = 1; i <= ans_Love; i ++) {
		if (P[i] == 0 && ans_Love_T[i] > 1) {
			ans ++;
			nLast = i;
		}
	}

	if (ans > 1 || ans == 0) {
		printf("-1\n");
		return 0;
	}
	
	for (int i = 1; i <= N; i ++) {
		if (Belong[i] == nLast) printf("%d ", i);
	}

	return 0;
}

↓↓↓ 有问题请在下方评论哦！ ↓↓↓

【Vijos 1626】爱在心中

Tags:

Status:

Share:

Comments: