

思考题:素数密度
给定区间[L,R] (L <= R <= 2147483647 ,R - L <= 1000000),计算区间中素数个数。
形如(2p-1)形式的素数成为麦森数,p为素数。
麦森数的性质:对于正整数n,当且仅当n能够被分解为若干个不同麦森数之积时,n的所有约数和为2的幂。
思考题:Fibonacci数列
已知 F1=1,F2=1,Fn=Fn-1+Fn-2。 现给出n,快速求Fibonacci数列的Fn.
分析:
朴素算法求Fn的时间复杂度为O(n),如果求出所有的Fn,这种方法已经是最优的了,但如果只求某一个Fn,可以用矩阵进行优化:
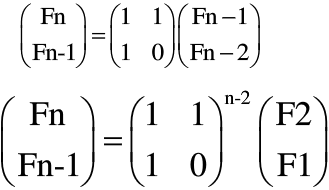
唯一质因子分解定理:合数a仅能以一种方式,写成如下的乘积形式:
a=p1e1p2e2…pnen(其中pi为素数,p1 < p2 < … pn,且ei为正整数)。
欧拉函数φ(m):设m是正整数,φ(m)表示1,2,3…m中与m互素的数的个数。
定理:若m=p1e1p2e2…pnen,则φ(m)=m(1-1/p1)(1-1/p2)…(1-1/pn)
假如a是一个整数,p是一个素数,那么ap≡a(mod p)
假如a不是p的倍数,ap-1≡1(mod p)(更常用)
若m,a为正整数,且m,a互素(GCD(m,a)=1),则aφ(m)≡1(mod m)
欧拉定理实际上是费马小定理的推广